
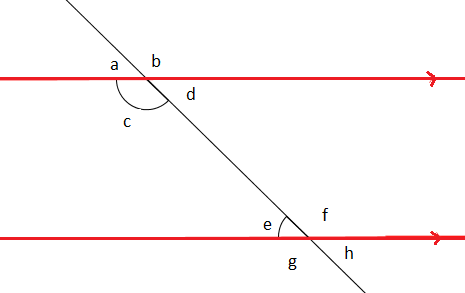
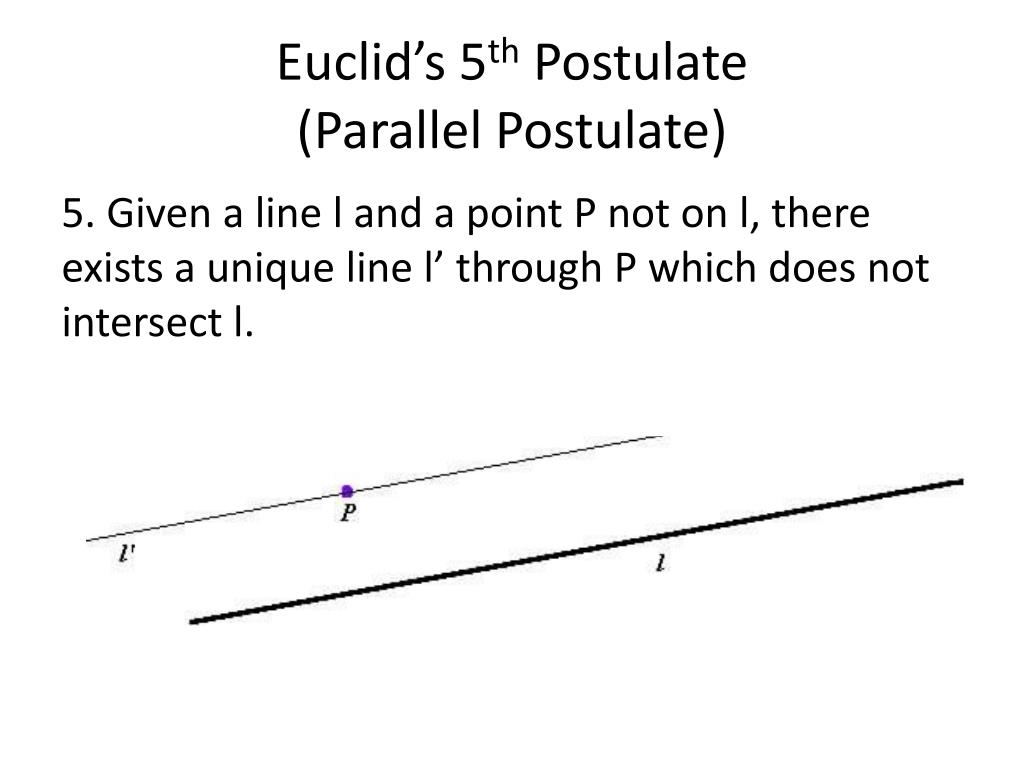
The two most important are Euclid's own formulation in his Postulate 5, which says that under certain conditions two lines meet, and Playfair's axiom (dating from 1795), which says there cannot be two distinct parallels to line L through the same point p. We consider three versions of Euclid's parallel postulate. With intuitionistic logic, there are two possible definitions of Euclidean fields, which turn out to correspond to different versions of the parallel postulate.
PARALLEL POSTULATE DEFINITION GEOMETRY HOW TO
We prove a similar theorem for constructive Euclidean geometry, by showing how to define addition and multiplication without a case distinction about the sign of the arguments. Classically, the models of Euclidean (straightedge-and-compass) geometry are planes over Euclidean fields. For example, in finding a perpendicular to line L through point P, one usually uses two different constructions, "erecting" a perpendicular when p is on L, and "dropping" a perpendicular when p is not on L, but in constructive geometry, it must be done without a case distinction. This involves finding "uniform" constructions where normally a case distinction is used. We show that Euclidean geometry can be developed using only intuitionistic logic.
Euclidean geometry, as presented by Euclid, consists of straightedge-and-compass constructions and rigorous reasoning about the results of those constructions.


 0 kommentar(er)
0 kommentar(er)
